Szögeltolódási képletek és megoldott gyakorlatok
az szögeltolás akkor keletkezik, amikor egy objektum egy kör alakú utat vagy utat követ. Ez eltér az elmozdulástól; míg a szögeltolódás méri az elmozdult szöget, az elmozdulás méri a távolságot.
A kerület mentén mozgó objektum szögeltolódásának kiszámításához kétféleképpen lehet használni: ha ismert a kezdeti és a végső szög, akkor a szögeltolás az utolsó szög és a kezdeti szög közötti kivonás lesz..
Ha ismert az elmozdulás hossza (a körív ívének hossza) és a kerület sugara, akkor a szögeltolódást θ = l / r adja meg..
index
- 1 képletek
- 2 Gyakorlatok
- 2.1 Első gyakorlat
- 2.2 Második gyakorlat
- 2.3 Harmadik gyakorlat
- 3 Referenciák
képletek
A fent leírt képletek megszerzéséhez az alábbi képek láthatók:
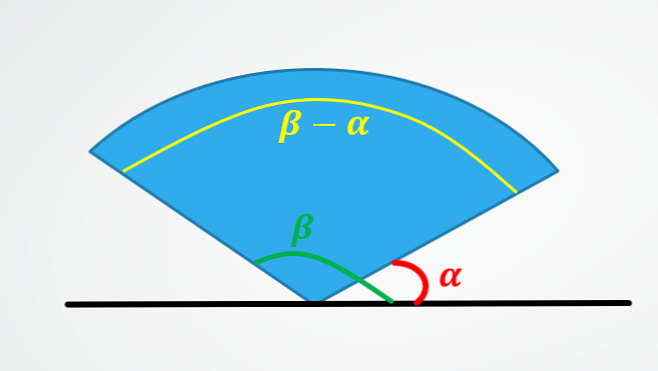
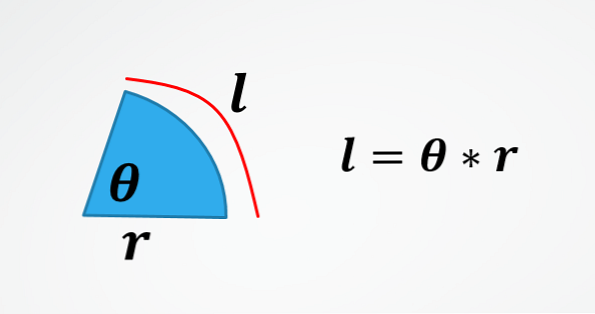
Az első azt mutatja, hogy miért egyenlő a szögeltolás az utolsó szög kivonásával, mínusz a kezdeti szög.
A második képen a körív hosszának képlete. Ezért az elszámolás θ segítségével az elején leírt képletet kapja meg.
edzés
Az alábbiakban néhány olyan gyakorlat, ahol a szögeltolás meghatározását kell alkalmazni, és ahol a fent leírt képleteket használják.
Első gyakorlat
Juan egy 35 méteres körúton fut egy kör alakú futópályán, amelynek sugara 7 méter. Számolja ki a Juan által elért szögeltolódást.
megoldás
Mivel a meghajtott ív távolsága és a kerület sugara ismert, a második képlet alkalmazható a Juan által végzett szögeltolódás ismeretére. A fent leírt képlet segítségével that = 35/7 = 5 radian.
Második gyakorlat
Ha van, hogy Mario utazott egy körkörös versenypályán, akkor mi a Mario szögletes elmozdulása??
megoldás
Ebben a gyakorlatban az első képlet kerül alkalmazásra. Mivel ismert, hogy Mario a pálya felét utazta, feltételezhető, hogy 0 ° -os szögben kezdte a versenyt, és amikor elérte a kör közepét, 180 ° -kal utazott. Ezért a válasz 180 ° -0 ° = 180 ° = π radián.
Harmadik gyakorlat
María körkörös medencével rendelkezik. A kutyád a medence körül fut 18 méteres távolságban. Ha a medence sugara 3 méter, mi a Maria kabalája által végrehajtott szögeltérés??
megoldás
Mivel a medence kör alakú, és ismeri annak sugárát, folytathatja a második képlet használatát.
Ismert, hogy a sugár 3 méter, és az állat által megtett távolság 18 méter. Ezért a végrehajtott szögeltolódás θ = 18/3 = 6 radian.
referenciák
- Basto, J. R. (2014). 3. matematika: Alapvető analitikai geometria. Patria Szerkesztői Csoport.
- Billstein, R., Libeskind, S., és Lott, J. W. (2013). Matematika: problémamegoldó megközelítés az alapfokú oktatók számára. López Mateos szerkesztők.
- Bult, B. és Hobbs, D. (2001). Matematikai lexikon (illusztrált szerk.). (F. P. Cadena, Trad.) AKAL kiadványok.
- Callejo, I., Aguilera, M., Martinez, L. és Aldea, C. (1986). Math. Geometria. Az E.G.B felső ciklusának reformja. Oktatási Minisztérium.
- Schneider, W. és Sappert, D. (1990). Gyakorlati műszaki rajz: az ipari műszaki rajz alapjainak bemutatása. Reverte.
- Thomas, G. B. és Weir, M. D. (2006). Számítás: több változó. Pearson oktatás.


