Colinear rendszer és példák

az colinear vektorok Ezek a meglévő vektorok három típusának egyike. Ezek azok a vektorok, amelyek ugyanabban az irányban vagy cselekvési vonalban vannak. Ez az alábbiakat jelenti: két vagy több vektor együttes, ha egymással párhuzamos egyenes vonalakban vannak elrendezve.

A vektort úgy definiáljuk, mint egy testre alkalmazott mennyiséget, és úgy jellemezzük, hogy egy irány, egy értelem és egy skála. A vektorok megtalálhatók a síkban vagy az űrben, és különböző típusúak lehetnek: colinear vektorok, párhuzamos vektorok és párhuzamos vektorok.

index

• 1 kolinális vektor
• 2 Jellemzők
  • 2.1 1. példa
  • 2.2 2. példa
  • 2.3 1. példa
• 3 Collinear vektor rendszer
  • 3.1 Kollektív vektorok ellentétes érzékekkel
  • 3.2 Az azonos értelemben vett kollináris vektorok
  • 3.3. Egyenlő nagyságú és ellentétes érzékekkel rendelkező kollináris vektorok
• 4 A colinear és a párhuzamos vektorok közötti különbség
• 5 Referenciák

Kollektív vektorok

A vektorok kollineárisak, ha az egyik vonala pontosan ugyanaz, mint minden más vektor, függetlenül az egyes vektorok méretétől és értelemétől..

A vektorokat reprezentációként használják különböző területeken, mint például a matematika, a fizika, az algebra és a geometria, ahol a vektorok csak akkor találhatók, ha irányuk megegyezik..

jellemzői

- Két vagy több vektor egymás mellett van, ha a koordináták közötti kapcsolat egyenlő.

1. példa

Az m = m_x; m_y és n = n_x; n_y. Ezek közösek, ha:

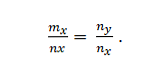
2. példa

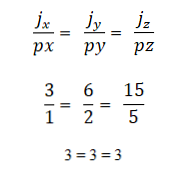
- Két vagy több vektor kollineáris, ha a termék vagy a vektorszaporítás nulla (0). Ez azért van, mert a koordinátarendszerben minden egyes vektorot a megfelelő koordináták jellemeznek, és ha ezek egymással arányosak, a vektorok kollinárisak lesznek. Ezt a következőképpen fejezzük ki:

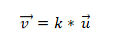
1. példa

A vektorok a = (10, 5) és b = (6, 3). Annak megállapítására, hogy azok kollináriálisak-e, a determináns elméletet alkalmazzák, amely meghatározza a kereszttermékek egyenlőségét. Ily módon:

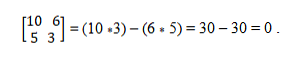
Colinear vektor rendszer

A colinear vektorok grafikusan vannak ábrázolva ezen irányok és értelemben, figyelembe véve, hogy át kell haladniuk az alkalmazási ponton és a modulon, amely egy bizonyos skála vagy hosszúság..

A kollináris vektorok rendszere akkor keletkezik, amikor két vagy több vektor egy objektumra vagy testre hat, és erővel bír, és ugyanabban az irányban jár..

Például, ha két kollináris erőt alkalmaznak a testre, ezek eredményei csak attól függnek, hogy milyen irányban működnek. Három eset létezik:

Collinear vektorok ellentétes érzékekkel

A két kollináris vektor eredményei megegyeznek ezek összegével:

R = Σ F = F₁ + F_2.

példa

Ha két erő hat a kosárra F₁ = 40 N és F₂ = 20 N az ellenkező irányban (a képen látható), az eredmény:

R = Σ F = (- 40 N) + 20N.

R = - 20 N.

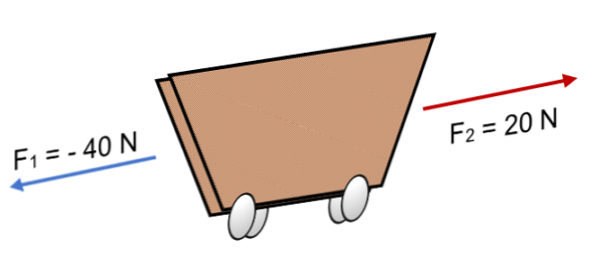
Az azonos értelemben vett kollináris vektorok

A kapott erő nagysága megegyezik a kollináris vektorok összegével:

R = Σ F = F₁ + F_2.

példa

Ha két erő hat a kosárra F₁ = 35 N és F₂ = 55 N ugyanabban az irányban (ahogy a képen látható), az eredmény:

R = Σ F = 35 N + 55N.

R = 90 N.

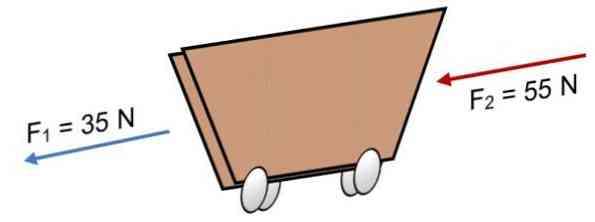
A pozitív eredmény azt jelzi, hogy a kollináris vektorok balra néznek.

Kollektív vektorok azonos nagyságú és ellentétes érzékekkel

A két kollináris vektor eredményei megegyeznek a kollináris vektorok összegével:

R = Σ F = F₁ + F_2.

Mivel az erők ugyanolyan nagyságúak, de az ellenkező irányban, azaz az egyik pozitív és a másik negatív, a két erő hozzáadásakor az eredmény egyenlő lesz nullával..

példa

Ha két erő hat a kosárra F₁ = -7 N és F₂ = 7 N, amelyek ugyanolyan nagyságúak, de ellenkező irányban (a képen látható), az eredmény:

R = ΣF = (-7 N) + 7N.

R = 0.

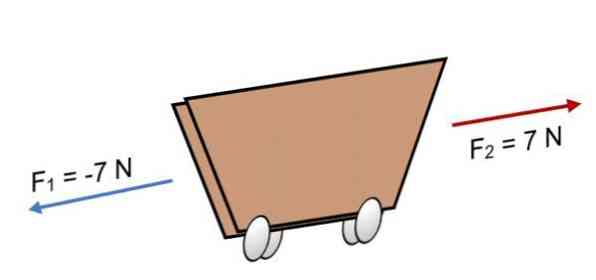
Mivel az eredmény 0, ez azt jelenti, hogy a vektorok egyensúlyban vannak egymással, és ezért a test egyensúlyban van vagy nyugszik (nem mozog).

A colinear és a párhuzamos vektorok közötti különbség

A kollináris vektorokat ugyanarra az irányra jellemzik, vagy egy vonalral párhuzamosan; azaz vektorok közvetlen párhuzamos vonalak.

Másrészt a párhuzamos vektorokat azért definiáljuk, mert azok különböző cselekvési vonalakban vannak, amelyeket egyetlen ponton fognak meg.

Más szavakkal, ugyanolyan származási vagy érkezési pontjuk van, függetlenül attól, hogy melyik modul, irány vagy irány -, és közöttük szöget alkotnak.

A párhuzamos vektorok rendszereit matematikai módszerekkel vagy grafikonokkal oldják meg, amelyek az erők párhuzamosságának és az erők sokszögének módszere. Ezen keresztül meghatározzuk a létrejövő vektor értékét, amely azt jelzi, hogy milyen irányba mozdul el a test.

Alapvetően a kolináris vektorok és a párhuzamos vektorok közötti fő különbség az a cselekvési vonal, amelyben cselekednek: a kollináriusok ugyanabban a sorban működnek, míg a párhuzamosak különbözőek.

Ez azt jelenti, hogy a kollináris vektorok egy síkban, "X" vagy "Y" -ban működnek; és a párhuzamos cselekedet mindkét síkban, ugyanabból a pontból kiindulva.

A kollináris vektorok nincsenek olyan pontban, mint a párhuzamosak, mert egymással párhuzamosak.

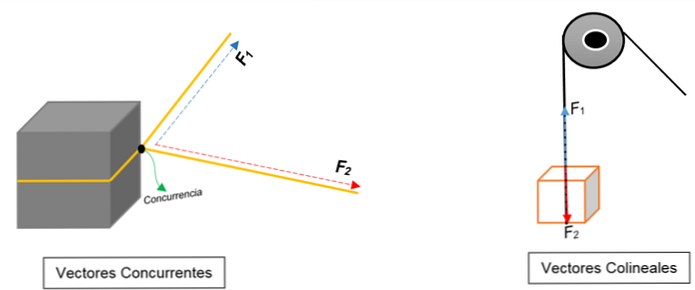
A bal oldali képen egy blokk látható. Egy kötéllel van kötve, és a csomó ketté osztja; amikor a különböző irányok felé és különböző erőkkel húzzák, a blokk ugyanabba az irányba mozdul.

Két vektor van ábrázolva, amelyek egy pontban (a blokkban) egyeznek meg, függetlenül attól, hogy melyik modul, értelem vagy irány.

Ehelyett a jobb oldali képen egy tárcsa jelenik meg, amely felemeli a dobozt. A kötél a cselekvési vonalat jelenti; húzáskor két erő (vektor) hat rá: egy feszültség ereje (amikor a blokkba mászik) és egy másik erő, a blokk súlyát kifejtő erő. Mindkettő ugyanolyan irányú, de ellentétes irányban; nem értenek egyet.

referenciák

1. Estalella, J. J. (1988). Vektor elemzés. 1. kötet.
2. Gupta, A. (s.f.). Tata McGraw-Hill oktatás.
3. Jin Ho Kwak, S. H. (2015). Lineáris algebra. Springer Science & Business Media.
4. Montiel, H. P. (2000). Fizika 1 a technológiai érettségért. Patria Szerkesztői Csoport.
5. Santiago Burbano de Ercilla, C. G. (2003). Általános fizika Szerkesztői Tebar.
6. Sinha, K. (s.f.). A matematika szövegkönyve XII. 2. Rastogi Kiadványok.