Archimedes életrajz, közreműködés és találmány
A Siracusa-i Archimedes (287 a.C-212 a.C) egy matematikus, fizikus, feltaláló, mérnök és görög csillagász volt a szicíliai szigeti ősi városból. Legjelentősebb hozzájárulása az Archimedes elve, a kimerítő módszer kifejlesztése, a mechanikai módszer vagy az első planetárium létrehozása..
Jelenleg az Euclides és az Apolonio mellett az ókori matematika három fontosabb alakja egyikének tekinthető, mivel a számítások, a fizika, a geometria és a csillagászat területén jelentős tudományos előrelépést jelentett. Ez viszont az emberiség egyik legjelentősebb tudósává teszi.

Habár a személyes életének kevés adata ismert, és az ismertek kétséges megbízhatósággal rendelkeznek, a közreműködései ismertek a műveiről és a mai napig megőrzött írásbeli levelekről. a levelezéshez, amelyet évekig tartott a barátokkal és az idő többi matematikusával.
Archimedes az idei híres volt a találmányaival, amelyek kortársai figyelmét felkeltették, részben azért, mert háborús eszközként használták, hogy sikeresen elkerüljék számos római inváziót..
Azonban azt mondják, hogy az egyetlen igazán fontos dolog a matematika volt, és a találmányai csupán az alkalmazott geometria időtöltésének termékei voltak. Az utókorban a tiszta matematika munkáit sokkal jobban értékelik, mint a találmányait.
index
- 1 Életrajz
- 1.1 Képzés
- 1.2 Tudományos munka
- 1.3 A konfliktus Siracusában
- 1.4 Halál
- 2 Archimedes tudományos hozzájárulása
- 2.1 Archimedes elve
- 2.2 Mechanikai módszer
- 2.3 A kar törvényének magyarázata
- 2.4. A tudományos demonstrációra vonatkozó kiürítési vagy kimerülési módszer kidolgozása
- 2.5 A kör mérete
- 2.6 A gömbök és a hengerek geometriája
- 3 találmányok
- 3.1 A kilométer-számláló
- 3.2 Az első planetárium
- 3.3 Az Archimedes csavar
- 3.4 Archimedes karja
- 4 Referenciák
életrajz
A Syracuse-i Archimedes kb. Kr. E. 287-ben született. Korai éveiről nem ismert sok információ, bár elmondható, hogy Syracuse-ban született, a város, amely ma Szicília szigetének fő tengeri kikötője, Olaszországban..
Abban az időben Syracuse volt az egyik olyan város, amely az úgynevezett Magna Grecia-t alkotta, amely a görög származású telepesek által lakott hely volt Olaszország és Szicília félszigetének déli részére..
Archimedes anyjával kapcsolatban nincsenek ismert tények. Az apával kapcsolatban ismert, hogy ezt Phidiasnak nevezték el, és hogy a csillagászatnak szentelte magát. Az apja információi ismertek a könyv egy töredékének köszönhetően A homokszámláló, Archimedes írta, amelyben említi az apja nevét.
Heraklides, aki görög filozófus és csillagász volt, nagyon szerette Archimedest, sőt még életrajzot is írt róla. Azonban ez a dokumentum nem került megőrzésre, így az abban található összes információ nem ismert.
Másrészről a Plutarco történész, filozófus és biográfus Parallel Lives című könyvében jelezte, hogy Archimedes vérviszonyban állt Hiero II-vel, egy olyan zsarnoksággal, aki Siracusában volt a Kr. E. 265 óta..
edzés
Az Archimedes-ről szóló kevés információ miatt nem tudjuk biztosan, hogy hol kapta meg az első képzést.
A különböző történetírók azonban megállapították, hogy nagy lehetőség van arra, hogy Archimedes Alexandriában tanult, amely a régió legfontosabb görög kulturális és oktatási központja..
Ezt a feltevést alátámasztja Diodoro Sículo görög történész adatai, akik jelezték, hogy Archimedes valószínűleg Alexandriában tanult..
Ezen túlmenően, számos munkájában Archimedes maga is említi az idő, amelynek munkája Alexandriában összpontosult, más tudósait, így feltételezhető, hogy ténylegesen ebben a városban fejlődött.
Néhány olyan személyiség, akivel Archimedes-nek valószínűleg kölcsönhatásba lépett Alexandriában, a földrajzi, matematikus és csillagász Eratosthenes of Cyrene, valamint a matematikus és a csillagász Conon de Sanos.
Családi motiváció
Másrészt, az a tény, hogy Archimedes apja csillagász volt, jelentős hatást gyakorolhatott a későbbi hajlamokra, mivel később és fiatal korban különleges vonzereje volt a tudomány.
Alexandriában töltött idejét követően becslések szerint Archimedes visszatért Siracusába.
Tudományos munka
Miután visszatért a Syracuse-ba, Archimedes kezdett különféle tárgyakat kidolgozni, amelyek hamarosan elnyerték egy bizonyos népszerűségét a város lakói körében. Ebben az időszakban teljes mértékben adta magát a tudományos munkához, különböző találmányokat készített, és számos matematikai fogalmat vont le, amelyek nagyon korán fejlettek.
Például, amikor a szilárd íves és lapos alakok jellemzőinek tanulmányozására szentelte magát, az integrált és differenciál kalkulusokkal kapcsolatos koncepciókat fogalmazott meg, amelyet később fejlesztettek ki.
Archimedes volt az is, aki meghatározta, hogy a gömbhöz kapcsolódó térfogat kétszerese a hengernek, amely tartalmazza azt, és az a személy, aki feltalálta a kompozit szíjtárcsát, a kar jogáról szóló felfedezése alapján..
Konfliktus Siracusában
Kr. E. 213-ban a római katonák beléptek Syracuse városába, és körülvették telepeseiket, hogy átadják őket.
Ezt a lépést a katonai és görög politikus, Marco Claudio Marcelo vezette a második büntetőháború keretében. Később római kardként ismerték, mivel végül Siracusát meghódította.
A két évig tartó konfliktus közepén a Syracuse lakói bátorsággal és hevesen harcoltak a rómaiakkal szemben, és Archimedes nagyon fontos szerepet játszott, tekintettel arra, hogy olyan eszközöket és eszközöket hozott létre, amelyek segítettek a rómaiak legyőzésében..
Végül Marco Claudio Marcelo felvette Syracuse városát. Archimedes nagy intellektualitása előtt Marcelo elrendelte, hogy ne sérüljenek meg vagy öljenek meg. Azonban Archimedeset egy római katona kezében ölték meg.
meghal
Archimedes 212-ben halt meg. Halála után több mint 130 évvel a Kr. E. 137-ben, az író, a politikus és a filozófus, Marco Tulio Cicero helyet foglal el Róma igazgatásában, és meg akarta találni Archimedes sírját.
Ez a feladat nem volt könnyű, mivel a Cicero nem talált senkit a pontos hely jelzésére. Azonban végül megkapta, nagyon közel az Agrigento ajtajához, és sajnálatos körülmények között.
Cicero megtisztította a sírját, és rájött, hogy egy gömb belsejében egy gömb belsejében íródott, hivatkozva az Archimedes által korábban elkészített kötet felfedezésére..
Változatok a haláláról
Első változat
Az egyik változat azt állítja, hogy Archimedes közepette megoldotta a matematikai problémát, amikor egy római katona megközelítette. Azt mondják, hogy Archimedes egy ideig feltehette volna, hogy megoldja a problémát, így a katona megölte volna.
Második változat
A második változat az elsőhez hasonló. Figyelembe véve, hogy Archimedes megoldotta a matematika problémáját, amikor a város felvétele történt.
Egy római katona belépett az összetételébe, és elrendelte, hogy találkozzon Marcelóval, és Archimedes azt válaszolta, hogy megoldania kell az első problémát. A katona ennek a válasznak a következtében megrémült, és megölte.
Harmadik változat
Ez a hipotézis azt jelzi, hogy Archimedesnek a matematikára jellemző eszközök nagy változatossága volt. Aztán egy katona látta őt, és azt hitte, hogy értékes tárgyakat hordoz, így megölte.
Negyedik változat
Ez a verzió azt mutatja be, hogy Archimedes a föld közelében volt, és terveket tervezett. Nyilvánvalóan hátulról jött egy római katona, és nem tudta, hogy Archimedes volt.
Archimedes tudományos hozzájárulása
Archimedes elve
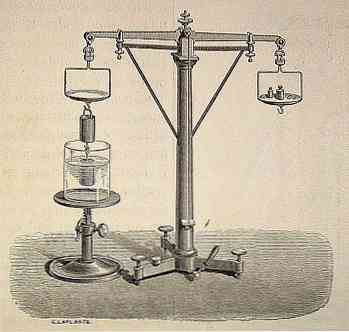
Archimedes elve a modern tudomány az ősi kor egyik legjelentősebb hagyatékának tekinthető.
A történelem folyamán, és szájon át, arról számoltak be, hogy Archimedes véletlenül felfedezte Hieron királynak köszönhetően, hogy meggyőződött arról, hogy egy aranykoronát, amelyet az általa gyártott, csak aranyat készített tiszta és nem tartalmazott más fémet. Ezt a koronát megsemmisíteném.
Azt mondják, hogy míg Archimedes meditál arról, hogyan oldja meg ezt a problémát, úgy döntött, hogy fürdik, és amikor belépett a fürdőkádba, rájött, hogy a víz szintje emelkedett, amikor belemerült belőle..
Ily módon felfedezheti azt a tudományos alapelvet, hogy "minden testben, amely teljesen vagy részben folyadékban (folyadékban vagy gázban) merül fel, felfelé irányuló tolóerőt kap, amely megegyezik az objektum által kiszabadított folyadék tömegével"..
Ez az elv azt jelenti, hogy a folyadékok felfelé irányuló erővel növekvő erőt fejtenek ki az őket beborító tárgyakra, és ennek a nyomóerőnek a mennyisége megegyezik az elmerült test által elhelyezett folyadék tömegével, függetlenül annak súlyától..
Ennek az elvnek a magyarázata a flotáció jelenségét írja le, és megtalálható abban Szerződés a lebegő testületekről.
Az Archimedes elve nagymértékben alkalmazandó a tömeges használatú tárgyak, például tengeralattjárók, hajók, életmentők és léggömbök úszására..
Mechanikai módszer
Az Archimedes egyik legjelentősebb hozzájárulása a tudományhoz egy tisztán mechanikai - azaz technikai - módszer felvétele a geometriai problémák megalapozásába és érvelésébe, ami példátlan módon jelentette az ilyen típusú problémák megoldását..
Archimedes kontextusában a geometriát kizárólag elméleti tudománynak tekintették, és a közös dolog az volt, hogy a tiszta matematika más gyakorlati tudományok felé irányult, amelyek alapelveit lehet alkalmazni..
Emiatt ma már a mechanika előfutárának tekinthető, mint tudományos fegyelem.
Az írásban, amelyben a matematikus az új módszert az Eratosthenes barátjának mutatja be, azt jelzi, hogy ez lehetővé teszi a matematika kérdéseinek kezelését mechanikán keresztül, és hogy valamivel könnyebb egy geometriai tétel bemutatása, ha már van van néhány előzetes gyakorlati ismerete, hogy ha nincs ötlete róla.
Az Archimedes által végzett új vizsgálati módszer a modern tudományos módszer felfedezésének és hipotézisének informális szakaszának előfutára lesz..
A kar törvényének magyarázata
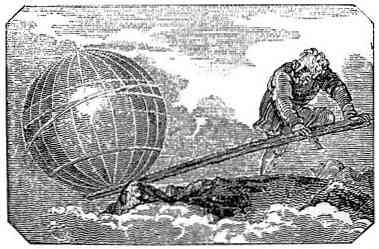
Míg a kar egy egyszerű gép, amelyet azóta sokkal korábban használtak, mint Archimedes, az ő az, aki megfogalmazta azt az elvet, amely elmagyarázza működését a síkon..
Ennek a törvénynek a megfogalmazásakor az Archimedes olyan elveket állapít meg, amelyek leírják a kar eltérő viselkedését két test elhelyezésekor, súlyától és távolságától függően..
Ilyen módon rámutat arra, hogy a karon elhelyezett két mérendő (arányos) test kiegyensúlyozott, ha a távolságuk fordítottan arányos a súlyukkal.
Hasonlóképpen, mérhetetlen testek (amelyek nem mérhetők) ezt teszik, de ezt a törvényt az Archimedes csak az első típusú testekkel bizonyította..
A kar alapelvének megfogalmazása jó példa a mechanikai módszer alkalmazására, hiszen a Dositeo-hoz irányított levélben elmagyarázza, hogy ez az első pillanatban a gyakorlatban alkalmazott mechanika módszereivel fedezhető fel..
Később megfogalmazta őket geometriai módszerekkel (elméleti). Ebből a kísérletezésből a testeken a gravitációs középpont fogalma is leválik.
A tudományos demonstrációra vonatkozó kiürítési vagy kimerülési módszer kidolgozása
A kimerülés olyan módszer, amelyet a geometriában használunk, amely a geometriai ábrák közelítéséből áll, amelyek területe a felirat és a körkörös leírás révén ismeretes egy másikra, amelynek területe ismert..
Bár Archimedes nem volt ennek a módszernek az alkotója, mesteri úton fejleszti, és sikerült kiszámítani a Pi értékét..
Archimedes, a kiürítés módszerével, a beírt és a körülhatárolt hatszögek átmérőjével 1, az abszurdra csökkentve a hatszögek és a kerület közötti területet..
Ehhez a hatszögeket osztotta fel, amelyek akár 16 oldalú poligonokat is létrehoztak, ahogy az előző ábrán látható.
Ily módon meghatározta, hogy a pi értéke (a kör hossza és az átmérő közötti kapcsolat) a 3.14084507 ... és a 3.14285714 értékek között van. .
Archimedes mesteri módon használta az exhaución módszerét, mert nemcsak sikerült közelítenie a Pi értékének kiszámítását egy hibahatárral, és ezért kívánatos volt, hanem azért is, mert Pi egy irracionális szám, ez a módszer és a kapott eredmények megalapozzák az alapokat, amelyek a végtelen számítási rendszerben csíráznak, és később a modern integrált számológépben.
A kör mérete
Egy kör területének meghatározásához az Archimedes olyan módszert használt, amely pontosan egy körbe illeszkedő négyzetet rajzol.
Tudva, hogy a tér területe az oldalainak összege, és hogy a kör területe nagyobb volt, elkezdett dolgozni a közelítés megszerzésében. Ezt úgy tette, hogy a négyzetet egy 6-oldalú sokszöggel helyettesítette, majd összetettebb poligonokkal dolgozott.
Archimedes volt az első matematikus a történelemben, hogy a Pi számát komolyan számolja.
A gömbök és a hengerek geometriája
Az Archimedes munkáját matematikában és fizikában összeállító kilenc tréning közül a gömbök és a hengerek geometriája két kötetet tartalmaz..
Ez a munka arra a megállapításra vonatkozik, hogy a sugár bármelyik gömbfelülete a legnagyobb körének négyszerese, és hogy a gömb térfogata kétharmada annak a hengernek a hányada, amelybe be van írva.
Inventos
A kilométer-számláló
Kilométerként is ismert, ez a híres ember találmánya volt.
Ezt az eszközt a kerék alapelve alapján építették, amely bekapcsolásakor aktiválja a sebességváltókat, amelyek lehetővé teszik a megtett távolság kiszámítását..
Ugyanezen elv szerint az Archimedes többféle típusú kilométert tervezett katonai és polgári célokra.
Az első planetárium
Sok klasszikus író, például Cicero, Ovid, Claudian, Marciano Capela, Casiodoro, Sexto Empirico és Lactantius tanúvallomása alapján sok tudós most Archimedesnek tulajdonítja az első kezdeti planetárium létrehozását.
Ez egy olyan mechanizmus, amelyet egy sor "szféra" alkot, amely képes volt a bolygók mozgását utánozni. Eddig a mechanizmus részletei nem ismertek.
Cicero szerint az Archimedes által épített planetáriumok kettő. Az egyikben reprezentálták a földet és a közelben lévő különböző csillagképeket.
A másikban, egyetlen forgatással, a nap, a Hold és a bolygók a független csillagokhoz képest önálló mozdulatokat tettek ugyanúgy, mint egy valódi napon. Az utóbbi esetben megfigyelhetőek a Hold egymást követő fázisai és elzáródásai is.
Archimedes csavarja
Az Archimedes csavar egy eszköz, amely alulról a tetejére a lejtőn keresztül vizet szállít, cső vagy henger segítségével.
Diodoro görög történész szerint a találmánynak köszönhetően megkönnyítette az ókori Egyiptomban a Nílus folyó mentén található termékeny földek öntözését, mivel a hagyományos eszközök hatalmas fizikai erőfeszítést igényeltek, ami kimerítette a munkavállalókat.
A használt henger egy azonos hosszúságú csavaron belül van, amely összekapcsolt egy propellert vagy uszonyrendszert, amely egy forgó karral hajtott, forgómozgást hajt végre..
Ily módon a hélixek minden anyagot az alulról felfelé tolnak, és egyfajta végtelen áramkört alkotnak.
Archimedes karja
Archimedes karmai vagy a vas-kéz, ahogy az is ismert, az egyik legfélelmetesebb háborús fegyver volt, amelyet a matematikus teremtett, és amely a római inváziók szicíliai védelme szempontjából a legfontosabb..
A Drexel Egyetem professzora, Chris Rorres (Matematika Tanszék) és Harry Harris (Építőmérnöki és Építészmérnöki Tanszék) által végzett kutatás szerint nagy kar volt, amely a karhoz csatlakozik. egy lánc segítségével, amely lógott belőle.
A karon keresztül a horgot úgy manipulálták, hogy az ellenséges hajóra esett, és a cél az volt, hogy akasztották fel, és olyan mértékben emeljék, hogy az elengedésekor teljesen felborulhasson, vagy a parton lévő sziklákra rúgjon..
Rorres és Harris bemutatták a "Gépek és különleges antik szerkezetek" című szimpóziumot (2001), egy "Egy hatalmas háborús gép: Archimedes vaskézének építése és működése" című miniatűr ábrázolását.
E munka megvalósításához Polibio, Plutarco és Tito Livio ősi történészek érveire támaszkodtak.
referenciák
- ASSIS, A. (2008). Archimedes, a tömegközéppont és a mechanika első joga [online]. Hozzáférés: 2017. június 10., bourabai.ru.
- DIJKSTERHUIS, E. (1956). Archimedes [online]. Hozzáférés a 2015. június 9-én elérhető World Wide Weben: books.google.co.ve/books.
- MOLINA, A. (2008). A Syracuse Archimedes kutatási módszere: intuíció, mechanika és exhaution [online]. Hozzáférés időpontja: 2017. június 10. a World Wide Webproduccioncientifica.luz.edu-nál.
- O'CONNOR, J. és ROBERTSON, R. (1999). Siracusa Archimedes [online]. Elérve 2017. június 9. a history.mcs.st-and.ac.uk oldalon.
- PARRA, E. (2009). Archimedes: élete, munkái és hozzájárulása a modern matematikához [online]. A lap eredeti címe: 2017. június 9., lfunes.uniandes.edu.co.
- QUINN, L. (2005). Siracusa Archimedes [online]. Hozzáférés: 2017. június 9., a math.ucdenver.edu.
- RORRES, C. & HARRIS, H. (2001). Félelmetes háborús gép: Archimedes vaskézének építése és üzemeltetése [online]. 2017 június 10-én került letöltésre a cs.drexel.edu címen.
- VITE, L. (2014). Archimedes elve [online]. A lap eredeti címe: 2017. június 10., a repository.uaeh.edu.mx.


