Heptagonális prizma jellemzők és a kötet kiszámítása

egy heptagonális prizma egy geometriai ábra, amely - ahogy azt a neve is jelzi - két geometriai meghatározást foglal magában: prizma és heptagon.

A "prizma" egy olyan geometriai alakzat, amelyet két alap egyenlő és párhuzamos sokszögek és oldalfelületeik párhuzamosak.

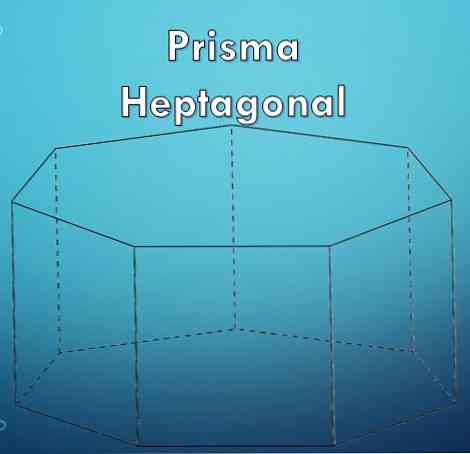
A "heptagon" egy sokszög, amelyet hét (7) oldal alkot. Mivel egy heptagon egy sokszög, lehet, hogy rendszeres vagy szabálytalan.

A sokszögnek rendszeresnek kell lennie, ha minden oldala azonos hosszúságú, és belső szögei azonosak, ugyanakkor az egyenlő oldalú sokszögeket is nevezik; különben azt mondják, hogy a sokszög szabálytalan.

A heptagonális prizma jellemzői

Az alábbiakban bizonyos jellemzők vannak, amelyek heptagonális prizmával rendelkeznek, mint például a felépítése, alapjainak tulajdonságai, az összes arcfelülete és térfogata.

1- Építés

Heptagonális prizma kialakításához két heptagon szükséges, amelyek a bázisok és a hét párhuzamossága lesz, egy a heptagon mindkét oldalán..

Kezdje a heptagon rajzolását, majd húzza meg a függőleges, egyenlő hosszúságú függőleges vonalakat, amelyek az egyes csúcsokból származnak.

Végül egy másik heptagon rajzolódik úgy, hogy a csúcsai egybeesnek az előző lépésben levő vonalak végével.

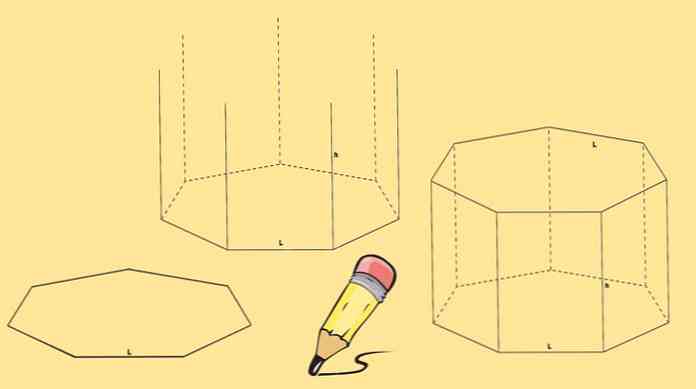
A fenti heptagális prizmát egyenes heptagális prizmának nevezik. De lehet egy ferde heptagális prizma, mint az alábbi ábrán látható.

2- A bázisok tulajdonságai

Mivel alapjaik heptagonok, megfelelnek annak, hogy az átlós szám D = nx (n-3) / 2, ahol "n" a sokszög oldalainak száma; ebben az esetben D = 7 × 4/2 = 14.

Azt is láthatjuk, hogy bármely heptagon (szabályos vagy szabálytalan) belső szögének összege 900º. Ezt a következő kép igazolja.

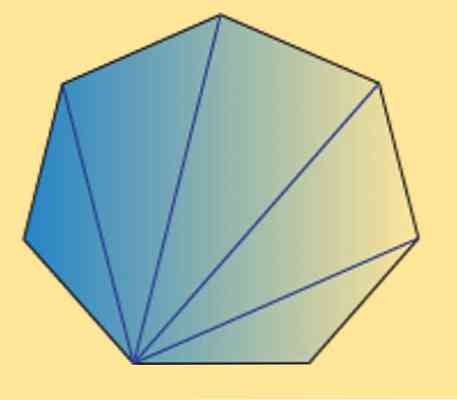
Mint látható, 5 belső háromszög van, és a háromszög belső szögeinek összege 180 ° -kal egyenlő, a kívánt eredmény elérhető.

3 - Heptagonális prizma létrehozásához szükséges terület

Mivel a bázisok két heptagon, és oldalai hét párhuzamosságot mutatnak, a heptagális prizma kialakításához szükséges terület 2xH + 7xP, ahol a "H" az egyes heptagonok területe és a "P" az egyes párhuzamos ábrák területe..

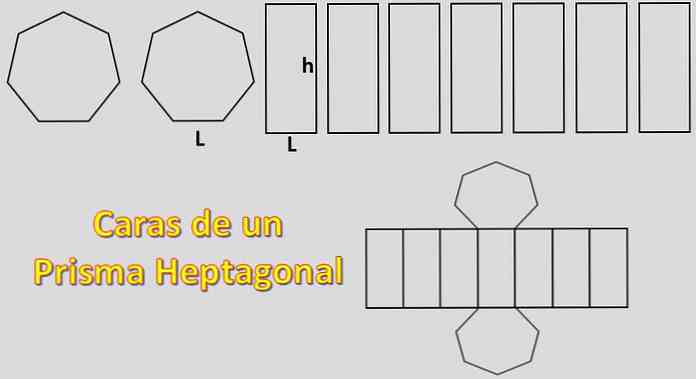
Ebben az esetben a rendszeres heptagon területét kiszámítjuk. Ehhez fontos tudni az apothema definícióját.

Az apothem egy merőleges vonal, amely egy szabályos sokszög középpontjától bármelyik oldalának középpontjáig megy.

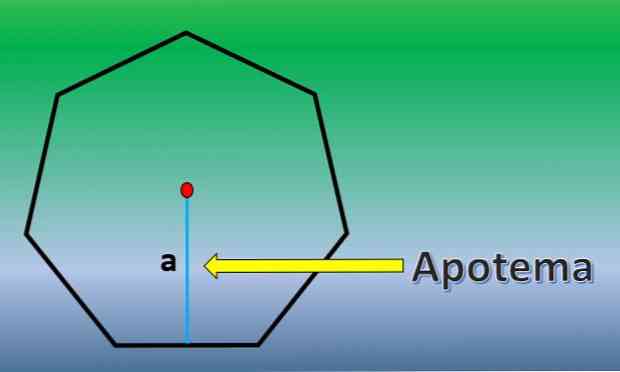
Amint az apothem ismert, a heptagon területe H = 7xLxa / 2, ahol az "L" az egyes oldalak hossza és "a" az apothem hossza..

A párhuzamos programterület területe könnyen kiszámítható, P = Lxh, ahol az "L" a heptagon és a "h" oldalának azonos hossza a prizma magassága..

Összefoglalva, a heptagális prizma (rendszeres bázisokkal) létrehozásához szükséges anyagmennyiség 7xLxa + 7xLxh, azaz 7xL (a + h).

4- Kötet

Miután ismert az alapfelület és a prizma magassága, a térfogat (alapterület) x (magasság).

Heptagonális prizma esetén (rendszeres bázissal) a térfogata V = 7xLxaxh / 2; V = Pxaxh / 2, ahol a "P" a normál heptagon kerülete.

referenciák

1. Billstein, R., Libeskind, S., és Lott, J. W. (2013). Matematika: problémamegoldó megközelítés az alapfokú oktatók számára. López Mateos szerkesztők.
2. Fregoso, R. S. és Carrera, S. A. (2005). Matematika 3. Szerkesztői Progreso.
3. Gallardo, G. és Pilar, P. M. (2005). Matematika 6. Szerkesztői Progreso.
4. Gutiérrez, C. T. és Cisneros, M. P. (2005). 3. matematikai kurzus. Szerkesztői Progreso.
5. Kinsey, L. és Moore, T. E. (2006). Szimmetria, alak és tér: a matematika bevezetése a geometrián keresztül (illusztrált, újranyomtatott). Springer Science & Business Media.
6. Mitchell, C. (1999). Káprázatos Math Line Designs (Illustrated ed.). Scholastic Inc..
7. R., M. P. (2005). 6 ° -ot rajzolok. Szerkesztői Progreso.